Lügen mit Statistik
Michael Holm sang 1974, dass Tränen nicht lügen – und er lag damit wahrscheinlich genau so daneben, wie jemand, der glaubt, Zahlen seien unbestechlich, Statistik zeige die Wahrheit und Wo eine Grafik zu sehen sei, da sei auch eine (richtige) Aussage zu erkennen.
„Ich traue keiner Statistik, die ich nicht selbst gefälscht habe“, soll Winston Churchill gesagt haben. Hat er aber wahrscheinlich nicht, denn dann fände sich irgendwo bestimmt ein Formulierung dieses Zitats im (englischen) Original – Churchill hat nämlich englisch gesprochen. Tut es aber nicht. Wir müssen uns wohl damit abfinden, dass der Ursprung dieses Bonmots unbekannt bleibt. Ist nicht schlimm. Allerdings steckt in diesem Aphorismus eine tiefe Wahrheit, denn tatsächlich lässt sich durch die FORM der Statistik und durch die Verwendung falscher Bezüge und Darstellungsmethoden – verbunden mit einer unkritischen Interpretation – die Realität als auch ihr Gegenteil darstellen. DARSTELLEN! Nicht beweisen!
Es gibt hunderte von Beispielen für verquere Statistiken – lustige und tragische. In der Folge ein paar besonders eindrückliche Beispiele. Wer sich für diese Thematik tiefergehend interessiert, dem sei das Buch „So lügt man mit Statistik“ von Walther Krämer empfohlen (Campus Verlag, ISBC 978-3-593-50459-9)
Scheinkausalität
99,99% (Achtung: Illusion der Präzision, siehe unten) aller Schulen arbeiten mit dem Begriff der Scheinkorrelation. Und begehen damit einen zwar nicht katastrophalen aber doch sinnentstellenden Fehler. Denn in den sogenannten Scheinkorrelationen besteht durchaus eine Korrelation (und zwar nicht nur zum Schein), aber der Zusammenhang der Daten, aus denen die Korrelation berechnet wird ist sinnlos – die Daten hängen nicht kausal voneinander ab. Darum heisst es richtigerweise: Scheinkausalität: es handelt sich um einen Fehlschluss.
Der Fachmensch (also ihr), nutzt den Begriff „Cum hoc ergo propter hoc“ (= mit diesem, folglich deswegen), eine richtige Korrelation und Kausalität zu bezeichnen, und „Cum hoc non est propter hoc“ (= mit diesem ist nicht deswegen), um eine Scheinkausalität bzw. Scheinkorrelation zu bezeichnen.
Was auf den ersten Blick kompliziert klingt, ist eigentlich simpel: Wenn zwei Dinge inhaltlich und nachweislich voneinander abhängen, das eine also das andere bedingt (und zwar zwingend), dann spricht man von einer Kausalität. Wenn zwei Ereignisse sich hingegen so entwickeln, dass ihre Entwicklungen gleich sind, einander aber nicht bedingen, dann spricht man von einer Scheinkausalität – oftmals begründet in der Gleichzeitigkeit von Ereignissen (= Koinzidenz). Ok, nochmals etwas einfacher: Häufig treffen zwei vollkommen unterschiedliche Ereignisse gleichzeitig auf, ohne dass sie etwas miteinander zu tun haben – stellt man nun die Entwicklung dieser Beispiele einander gegenüber, so schein (sich!) es so, als würden sie voneinander abhängen und sich gegenseitig beeinflussen. Tun sie aber nicht.
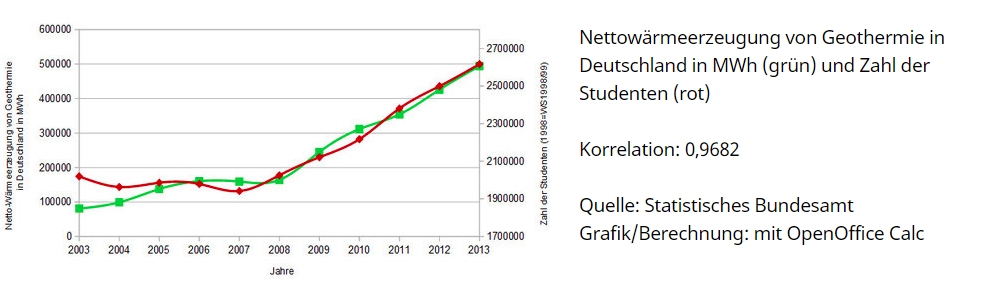
Je mehr Geothermie erzeugt wird, desto mehr Studenten gibt es – na klar. Quelle: www.scheinkorrelation.jimdo.com / Norman Zellmer
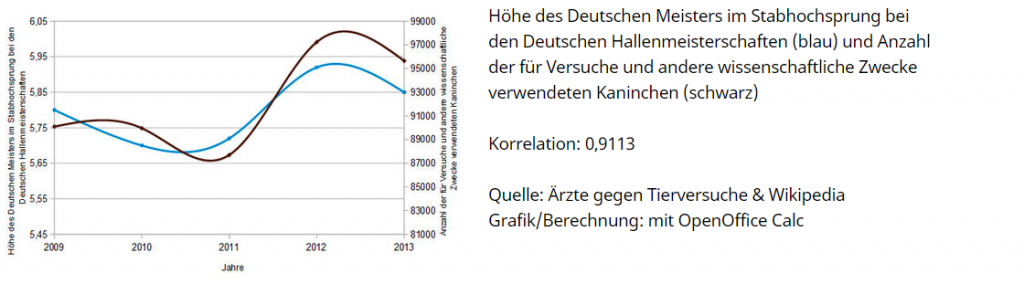
Abhängigkeit zwischen Hochsprung und Versuchskaninchen. Quelle: www.scheinkorrelation.jimdo.com / Norman Zellmer
Bei so blöden Beispielen ist es auf den ersten Blick klar, dass da eine Scheinkausalität vorliegt (trotz der unbestreitbar rechnerisch vorhandenen Korrelation). Diese doofen Beispiele sind deshalb auch nicht gefährlich. Wenn aber Kriminalitätsraten, Ausländerzahlen oder Krankheitsbilder mit Schokoladenkonsum in Zusammenhang gebracht werden, ohne zu prüfen, ob dieser Zusammenhang gegeben ist, dann wird es grobfahrlässig bis böswillig.
Es ist aber eine weit verbreitete Vorgehensweise aller(!) politischer Parteien, ihre Ansichten pseudo-wissenschaftlich zu untermauern und als glaubhaft erscheinen zu lassen. Mit abnehmender Intelligenz der Botschaftsempfänger werden diese Ansichten zunehmend bereitwilliger angenommen (ok, das ist eine Kausalität, deren Echtheit noch abschliessend bewiesen werden müsste…)
Ein aktuelles Beispiel: Eine dänische Forschergruppe hat herausgefunden, dass die Selbstmordrate von Menschen, die in Hochhaussiedlungen leben, höher ist, als bei Menschen, die in Einfamilienhäusern leben. Messerscharf hat die Gruppe analysiert, dass „grün“ offenbar eine positive Wirkung auf das Wohlbefinden habe und vorgeschlagen, die Bewohner von grauen Wohnsilos sollte zumindest eine Wand in ihrer Wohnung grün streichen – Kommentar überflüssig.
Und weil es so schön ist, noch ein Beispiel für Scheinkausalität. Man hat herausgefunden (was nicht so schwierig war), dass die meisten Alkoholiker (also Männer) verheiratet sind. Ergo kann man schlussfolgern, dass die Frauen die Hauptursache für Alkoholismus bei Männern sind – DAS ist Scheinkausalität.
„Lügen“ mit Präzision
Wir sind uns gewöhnt, dass runde Zahlen immer falsch sind. Haben wir so gelernt – das kriegen wir aus unseren Köpfen so gut wie nicht raus. „Round numbers are always false“, das hat sich eingeprägt. Ich habe noch nie eine Telefonrechnung über 100.- Euro bekommen, habe noch nie eine Runde Zahl an Steuern bezahlt, und beim Einkaufen zahle ich auch so gut wie nie runde Summen (Nur Verkehrsbussen sind „rund“ – entsprechend negativ sind sie bei mir verankert).
Wir ziehen aus diesen Erfahrungen unbewusst den (falschen) Umkehrschluss, dass ungerade Zahlen die Wahrheit viel genauer wiedergeben. Das ist faktisch natürlich Blödsinn, wird aber häufig genutzt, um den Eindruck von Wahrheit eine Aussage zu erwecken. Das ist allerdings keine neue Erkenntnis, dieses Gefühl der „Wahrheit des Präzisen“ : Adam, so steht es schon in der Bibel (AT, Genesis, 5.3ff), wurde 930 Jahre alt, Seth (für alle, die nicht bibelfest sind: das ist ein Sohn von Adam und Eva) 912 Jahre, Jered (seinerseits ein Nachkomme von Seth) wurde 962 Jahre alt… die wurden nicht etwa „sehr alt“, das wäre wohl zu wenig eindrücklich – also wurde ihnen ein wahrhaft biblisches Alter angedichtet, das bei den Gläubigen einen besonders starken Eindruck hinterlassen sollte (und wohl auch gleichzeitig belegen, dass der Autor quasi „mit dabei war“).
Wir können mit ziemlich gutem Grund behaupten, dass präzise Zahlen wohl präzise sind, aber keine vernünftige Aussagekraft beinhalten. Wem nützt es schon, wenn wir wissen, dass „der Deutsche“ im Jahr durchschnittlich 61,45kg Fleisch ist? Was ist der Informations- und Wahrheitsgehalt der zweiten Nachkomma-Stelle? Null! Niente! Nada!.
Die Präzisions-Sucht findet man übrigens auch in Fallstudien-Lösungen: Dann, wenn irgendwelche Prozente (die in der Ausgangsform ohne Kommastelle vorliegen) nach dem vierten Rechenschritt plötzlich 3, 4 oder noch mehr Nachkommastellen aufweisen – und damit den Eindruck erwecken (sollen), dass präzise gerechnet wurde. Aber: man merkt die Absicht und ist verstimmt – schlussendlich ist diese Art, ein Resultat anzugeben, nur der Beleg, dass jemand nicht mit Kommastellen umgehen kann.
Faustregel: Nie mehr Kommastellen als unbedingt notwendig – und dafür gibt es auch eine Regel:
- Beim Strichrechnen: Das Resultat hat maximal so viele Komma stellen wie der Ausgangswert mit den meisten Nachkommastellen (also: 4,25 + 1,2 = 5,45)
- Beim Punktrechnen (potenzieren gehört auch dazu): Die Anzahl der Kommastellen der einzelnen Werte wird addiert
1,2 x 1,2 = 1,44
5,0 / 1,2 = 4,17 (und nicht: 4,166)
Unsägliche Mittelwerte
Zwei Männer sitzen im Wirtshaus, der eine zwei Schweinshaxen, der andere trinkt zwei Maß Bier. Statistisch gesehen hat also jeder eine Haxe und ein (sehr) grosses Bier getrunken. Aber der eine hat sich überfressen und der andere ist besoffen (frei nach: Franz-Josef Strauß).
Mit Mittelwerten ist es so eine Sache – sie sind hervorragend geeignet, um Tatsachen zu verfälschen und bleiben deswegen rein rechnerisch dennoch richtig. Ideal, um eigene Einstellungen und Sichtweisen in pseudo-wissenschaftlicher Art zu vermitteln. Im Klartext: Ein Mittelwert ohne Angabe der Streuung ist sehr wenig bis gar nichts wert.
Verfälschende Aussagen mit Mittelwerten
In Plymouth/England beträgt die Tagesdurchschnittstemperatur im Jahr rund Grad Celsius – etwa gleich hoch liegt die Durchschnittstemperatur in Minneapolis/USA
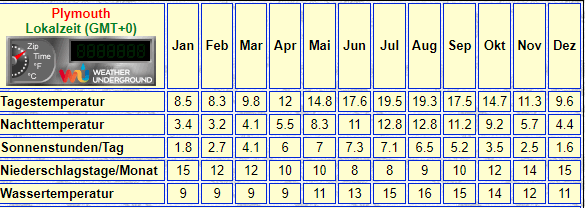
An den Daten ist nichts auszusetzen – wenn man sie korrekt vergleicht.
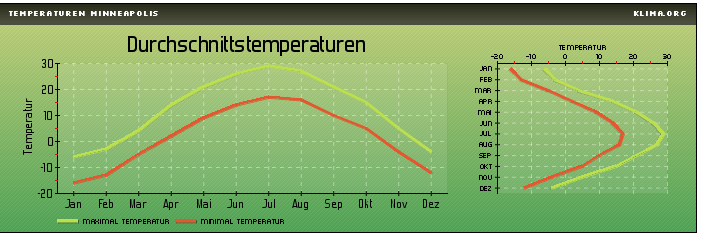
Mit Durchschnittswerten kann man ziemlichen Unsinn anstellen.
Während in Plymouth aber ein relativ ausgeglichenes Klima herrscht, kann es in Minneapolis auch schon mal -20 Grad kalt werden, und 40 Grad im Sommer sind auch keine Seltenheit – es kann also keine Rede davon sein, dass die beiden Orte das gleiche Klima haben, trotz gleichen Durchschnittswertes (arithmetisches Mittel)
Ein Wirt wurde gefragt, woraus denn sein Wildkaninchenragout genau bestehe. „Nun ja“, sagte dieser „um ehrlich zu sein, ist da auch ein wenig Pferd mit dabei – wegen des Geschmacks.“ Aha – und wie wieviel Pferdefleisch? „Halb-Halb“ sagte der Wirt. „Ein Kaninchen, ein Pferd“. (arithmetisches Mittel)
Nehmen wir ein anderes Beispiel: Kennt jeder! „Was ist sicherer? Das Reisen mit dem Flugzeug oder das Reisen mit der Bahn?“ (Wir fragen bewusst nicht nach dem Auto – autofahren ist ja quasi Selbstmord. Statistisch gesehen. Weiss jeder.)
Ihr kennt natürlich die Antwort: Fliegen ist sicherer – denn wir kennen alle die Statistik, die so oder so ähnlich aussieht:
Bahn: 18 Verkehrstote pro 100 Milliarden Passagier-Kilometer
Flugzeug: 9 Verkehrstote pro 100 Milliarden Passagier-Kilometer
Wussten wir es doch, fliegen ist doppelt so sicher. Und die Angsthasen mit Flugangst sind halt vollkommen irrational. Naja – wir könnten ja auch, und zwar mit dem gleichen Recht (mindestens!) nicht nach den Anzahl Passagier-Kilometern fragen, sondern nach der Zeit, die man im jeweiligen Reisemittel verbringt – und voilà:
Bahn: 7 Verkehrstote pro 100 Millionen Passagier-Stunden
Flugzeug: 24 Verkehrstote pro 100 Millionen Passagier-Stunden.
Auf den Zeitfaktor bezogen ist Fliegen also mehr als 3x gefährlicher als fliegen. Nur mal so.
Mit Prozenten bluffen
„Prozent“ – das hat doch was von „berechnet, daher genau“. Prozente vermitteln Glaubwürdigkeit, Seriosität und Sicherheit. Dabei muss einem klar sein, dass ein Prozentwert grundsätzlich 50% der Informationen verschluckt – zu Beginn haben wir zwei Werte: Zähler und Nenner – hinten kommt eine Zahl raus, der Prozentwert bzw. der Quotient. Es fehlen also zwangsläufig die Bezugswerte, um einen Prozentsatz, der für sich alleine steht, vernünftig einschätzen zu können. Und so wird gerne einer kleinen Zahl ein Prozent-Mäntelchen umgelegt und schon erscheint sie riesengross. Politiker machen das besonders gerne, aber nicht nur die.
„Wir haben die Frauenquote unserer Vorstandsmitglieder innerhalb von 5 Jahren um 50% steigern können!“ – toll. Jetzt sind es 3 statt wie bisher 2!
„Gefährliche Cholera-Keime in der Ostsee! Verdoppelung der Cholera-Gefahr in Deutschland befürchtet! (Hamburger Abendblatt) – Panik! Wahrscheinlich sind die Ausländer schuld! Nun gut, aktuell erkranken in Deutschland 2 Personen pro Jahr an Cholera (meistens nach einer Auslandreise), im schlimmsten Fall wären es dann also 4 – nicht schön für die Betroffenen, aber jetzt wirklich auch kein Grund für eine Volkspanik – ausser vielleicht bei der AfD.
Nehmen wir mal an, unsere Firma dümpelt so vor sich hin. 2016 hatten wir einen Umsatz von 100 kCHF, 2017 101 kCHF und 2018 102,5 kCHF – eine dynamische Entwicklung ist das nicht wirklich. Was tun? Vorschlag: Wir nennen nicht die Wachstumsraten sondern die Wachstumsraten der Wachstumsraten. Im ersten Jahr wuchs unser Unternehmen um 1%, im zweiten um 1,49% – wir können also von 2017 auf 2018 eine Zunahme des Umsatzwachstums von 49% ausweisen. Bäääm!
Es gibt übrigens auch einen vernünftigen Grund, warum Krankenkassen vermelden, ihr Beitragssatz wachse von 13 auf 14% (wir sprechen hier von Deutschland), also um nur einen Prozentpunkt. Dass es sich dabei um 1/13 handelt, also um 7,7% – das sagen sie lieber nicht.
In einer Landwirtschaftszeitung war einst zu lesen: „Deutsche Kühe geben immer weniger Milch!“ – etwas genauer gelesen, war zu erfahren, dass Milchkühe 1990 im Schnitt 4700 Liter Milch gegeben hatten, im Jahre 2000 5200 Liter, im Jahre 2010 noch 5500 Liter – eine Abnahme der Zunahme von 300 Litern oder 40%. „Weniger“ ist etwas anders.
Trends vernebeln den Blick
Der Mensch generell hat ein Problem bei der Beurteilung von Veränderungen: Wir gehen (fast) immer davon aus, dass alles so weiter geht, wie es angefangen hat. Nur in ganz wenigen Fällen ist uns klar, dass das nicht stimmt – in den meisten Fällen aber nicht.
Mit Extrapolationen – so nennt man das „hochrechnen“ von Veränderungen – tun wir uns unglaublich schwer und entsprechend auch mit dem Erkennen von diesbezüglichen Fehlinterpretationen – genau gleich wie wir das bei Scheinkausalitäten tun. Mit nichts kann man so gut Stimmung machen, wie mit einer Extrapolation, weil sie so schön einfach ist – und man kann (ich hacke jetzt nochmal auf den Parteien und Politikern rum) immer noch den Satz hinten dranhängen: „Nur Blinde und Idioten sehen das nicht!“ – Vorzugsweise extrem rechte und extrem linke Parteien nutzen dieses Totschlagargument.
Wir sind mental träge, wir schliessen von dem, was wir überblicken können auf das was war und auf das, was sein wird – wir nehmen schlicht und einfach gerne an, dass alles schon immer so gewesen ist und auch immer so bleiben wird. Vor allem Entwicklungen. Wir vergessen dabei, dass in sehr vielen Fällen die Annahmen, die unseren Überlegungen zugrunde liegen, falsch sind. Und das führt uns nicht selten vollkommen in die Irre und lässt uns auch noch im Glauben, wir hätten recht – weil alles so schön logisch aussieht. Trends sind allenfalls kurzfristig(st) tauglich – sonst nicht.
„Trendexplorierer sind Autofahrer, die nachts ohne Licht auf einer geraden Strasse fahren – sie haben nur solange Glück, wie keine Kurve kommt.“ (So lügt man mit Statistik, S. 88)
Um mit Trends den klaren Blick zu trügen, bedient man sich gerne der Verzerrung von Achsen in graphischen Darstellungen.
Donald Trump und Angela Merkel machen einen Wettlauf. Merkel gewinnt. In Deutschland kann man in den Zeitungen lesen: Die Bundeskanzlerin und der amerikanische Präsident haben sich einen Wettlauf geliefert, den Angela Merkel für sich gewinnen konnte.
Fox News vermeldet: Unser aller Präsident Donald Trump hat an einem Wettkampf teilgenommen, an dem auch die deutsche Bundeskanzlerin Angela Merkel teilnahm. Nach einem furiosen Rennen konnte Trump den hervorragenden 2. Platz erobern, während die Deutsche Vorletzte wurde.
Piktogramme: Die Boulevard-Version der Statistik
Die Macht des (manipulierenden Bildes) nutzen vor allem Medien. Mit Piktorgrammen lassen sich nämlich auf subtile Art Verhältnisse und Veränderungen vollkommen anders darstellen, als sie in Wirklichkeit sind. Hier reichen ein paar Beispiele – sie sind selbstentlarvend.
Tendenzöse Berichterstattung durch falsche Bezugswerte
Schlagzeile: „Alarm! Die Waldfläche in der Schweiz nimmt dramatisch ab!“ – Erklärtext: 1960 betrug die Waldfläche in der Schweiz noch 2.120 m2 pro Million Einwohner, heute, 2019 ist diese Zahl dramatisch gesunken und beträgt nur noch 1,627 km2 – das ist ein Rückgang von fast einem Viertel! Wenn das so weitergeht, dann verschwindet der Wald in der Schweiz bald ganz!!!
Ähm ja, so kann man es natürlich auch sehen – oder kommunizieren. Die Faktenlage ist allerdings eine andere: Die Waldfläche in der Schweiz betrug 1960 rund 11.250 km2, im Jahr 2018 betrug die Fläche 13.700 km2 (ist also um etwa 20% gestiegen). In der gleichen Zeit hat die Bevölkerung allerdings von 5,3 auf 8,4 Millionen zugenommen (Quelle: bfs und waldschweiz.ch).
Was wir hier haben ist eine klassische tendenziöse Berichterstattung – es wird ein Bezugswert ins Feld geführt, der überhaupt keinen Einfluss auf die Faktenlage hat. Durch einen solchen Bezug wird aber Stimmungsmache betrieben. In diesem Fall: „Das Boot ist voll“ – es wird bewusst der Eindruck erweckt, die zunehmende Bevölkerung holze Wälder im großen Stil ab, um Wohnraum zu schaffen. Übrigens: das Beispiel ist frei erfunden, es ist mit einer anderen Thematik aber mit dem gleichen Bezugsfehler allerdings mehrfach in der Weltwoche kommuniziert worden.
Und noch ein paar Beispiele
(Hier: Armut und anderes aus den beiden Büchern)

