Damit wir sinnvolle Rückschlüsse auf die Grundgesamtheit ziehen können, braucht es in der Praxis also mehr als nur Repräsentativität – es braucht noch die Wahrscheinlichkeitsberechnung. Wir wollen ja wissen, wie genau unsere Rückschlüsse vermutlich sein werden und wie wahrscheinlich es ist, dass unser Ergebnis auch stimmt.
Um herauszubekommen, wie wahrscheinlich ein Ergebnis ist, benötigen wir die Wahrscheinlichkeitsrechnung, und einen Prozentwert, der uns angibt, wie hoch die Wahrscheinlichkeit ist, dass unser Ergebnis stimmt.
Um herauszubekommen, wie genau (also eigentlich: wie gut) unser Ergebnis sein wird, benötigen wir das so genannte Signifikanz-Niveau. Das bedeutet nichts anderes, als die prozentuale Angabe, zu wie vielen % wir uns maximal irren möchten. Wie gross dieser Wert ist, hängt davon ab, was wir untersuchen – wenn wir untersuchen wollen, ob das Tragekabel einer Luftseilbahn die Kabine halten kann, dann möchten wir uns hoffentlich nicht um 5% irren – wenn wir andererseits die Kaufbereitschaft für Zahnpasta abklären möchten, dann ist eine Irrtumswahrscheinichkeit von 5% durchaus ausreichend um uns mal einen groben Überblick und eine ebensolche Schätzung zu ermöglichen.
Um die Irrtumswahrscheinlichkeit anzugeben, nutzen wir „Sigma“. Den kann man berechnen, aber erst gegen Mitte eines Mathematikstudiums – wir lassen das also. Ausserdem gibt es dafür Tabellen – das lassen wir auch, denn uns interessieren im Allgemeinen lediglich 3 Werte
- Sigma 1 = 68,2% (Standardabweichung: +/- σ)
- Sigma 2 = 95,4% (Standardabweichung: +/- 2 σ)
- Sigma 3 = 99,7% (Standardabweichung: +/- 3 σ)
(Dieser Wert wird in der Stichprobenberechnung meistens mit „t“ angegeben)
Woher aber kommen diese Werte? Es hilft dem Verständnis, wenn man sich diese Frage nicht nur stellt, sondern auch beantwortet. Diese Werte entstammen der Normalverteilung und die %-Werte bezeichnen die Fläche (also auch die Ereignisse), die sich unterhalb einer normalverteilten Kurve innerhalb einer bestimmten Breite befinden. In der Mitte befinden sich die meisten Ereignisse, nach links und rechts werden es immer weniger – weil es extreme Werte sind, und extreme Werte gibt es nun mal weniger, als „normale“ Werte.
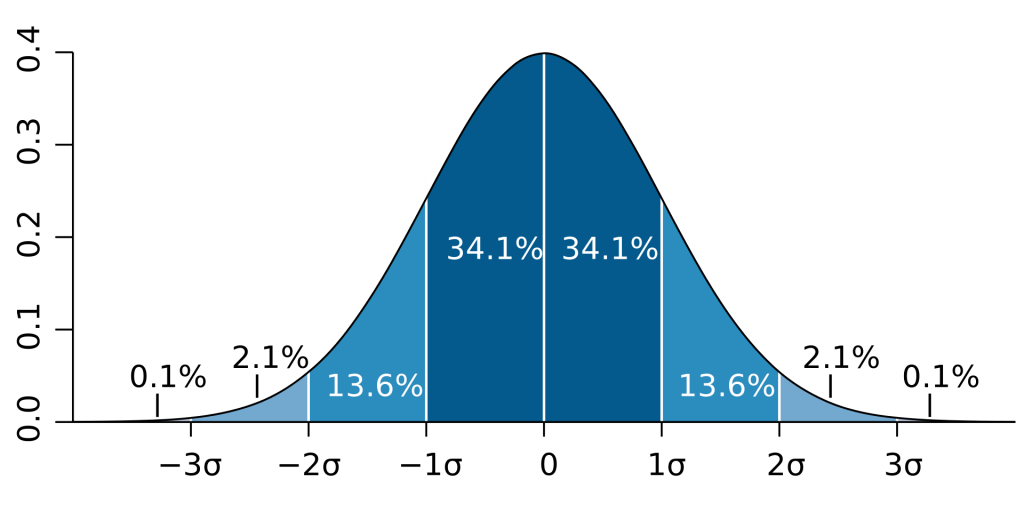
Die beiden Teilflächen links und rechts der Mitte gehören zusammen (deshalb auch +/-)

